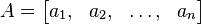The Cafes

I hate 1% problems. No this isn’t an OWS slogan. I’m thinking of those code issues that really aren’t a problem 99% of the time, but when they bite, they’re really hard to debug and they cause real pain. Several common cases in Java:

1. Using java.util.Date or java.util.Calendar instead of JodaTime.
2. Not specifying a Locale when doing language sensitive operations such as toLowerCase() and toUpperCase().
3. Not escaping strings passed to SQL, XML, HTML or other external formats.

What I hate most is that it’s really, really hard to convince other developers that these are problems they should take seriously. Read the rest of this entry »

Last week one of my colleagues hit me with an idea that was so obvious when he pointed it out I wondered why I hadn’t realized it before:

If you’re designing for reuse, you’re doing it wrong.

In 2012 the only code you should be writing is what’s needed for the immediate task at hand. Don’t design for reuse. Don’t consider reuse. Don’t waste one minute of your day making code reusable.
Read the rest of this entry »

One of my better math teachers in high school was John Brumfield. He taught me Algebra I and Precalculus. He was also exceptional at calculation, a skill that got him into in the artillery core in World War II, where he had to calculate gunnery firings in real time. And he had a great sense of humor. But one of the things that stands out most clearly in my memory from one of his classes is something he may have gotten wrong (perhaps deliberately). At that point in the early 1980s scientific calculators existed, but were quite expensive and not yet integrated into the high school mathematics curriculum. We were probably one of the last classes to spend significant time learning about trig tables, and how to interpolate between values. (A surprisingly useful skill, by the way, even if the reason we learned it no longer applies.) I recall that someone in the class asked him how the numbers in the tables were calculated. E.g. how did the author know that the sine of 47.1 degrees was 0.0238875315 and not 0.0238875326 or some other value? And his answer still sticks with me to this day, and I quote it word for word: “Very accurate graphs”.
Read the rest of this entry »

If we follow Wikipedia in defining a cyclic group as a group in which there exists an element g in G such that G = <g> = { gⁿ | n is an integer }, then the integers under addition are clearly a cyclic group with the generator 1. But why do we define cyclic groups that way? Or, another way of putting it, why is the definition given the name cyclic when there’s nothing cyclic about it?
Read the rest of this entry »

I was watching Gilbert Strang’s 18th lecture in 18.06 Linear Algebra a couple of days ago, and he laid out a theory of determinants that started from a few basic properties and derived all the usual results. However he provided essentially no motivation for what he was doing. Why these properties? How did any one ever think of these particular axioms? And more tellingly, what is a determinant, really? I don’t mean the official definition (here quoted from Wikipedia and similar to Strang’s):

If we write an n-by-n matrix in terms of its column vectors

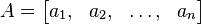
where the a_j are vectors of size n, then the determinant of A is defined so that

where b and c are scalars, v is any vector of size n and I is the identity matrix of size n. These properties state that the determinant is an alternating multilinear function of the columns, and they suffice to uniquely calculate the determinant of any square matrix. Provided the underlying scalars form a field (more generally, a commutative ring with unity), the definition below shows that such a function exists, and it can be shown to be unique.

I can follow the derivation from that, but it doesn’t really explain what a determinant is. And the only alternative I could find in Wikipedia or the readily available textbooks, was that it’s the volume of a parallelepiped of the matrix formed by the vectors representing the parallelepiped’s sides. Again, that feels like a derived property, not a true definition. However, Mathworld, did give me one big hint:

For example, eliminating x, y, and z from the equations
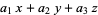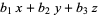= 0
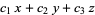= 0
= 0
gives the expression

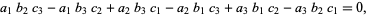
which is called the determinant for this system of equation.

So here’s the answer: the determinant is the condition under which a set of linear equations has a non-trivial null space. Or, more simply, the determinant is the condition on the coefficients a, b, c… of a set of n linear equations in n unknowns such that they can be solved for the right hand side (0, 0, 0, …0) where at least one of the unknowns (x, y, …) is not zero. Let me prove that:
Read the rest of this entry »